The electrical power system in the United States is at a crossroads between its mission to deliver cheap and safe electrical energy, a strategic aim to increase the penetration of renewable energy, an increased reliance on smart grid technology, and the critical need to maintain and increase the grid’s reliability. As well, the operation and planning of the grid with these requirements involves an unprecedented amount of uncertainty in supply and demand brought on by the high variability of wind, solar, and other renewable power sources. This project will develop advanced optimization methods for optimal operation of the power grid under uncertainty. This will allow answering, at full resolution, important questions such as: Can 20% wind power penetration be achieved without compromise for reliability?

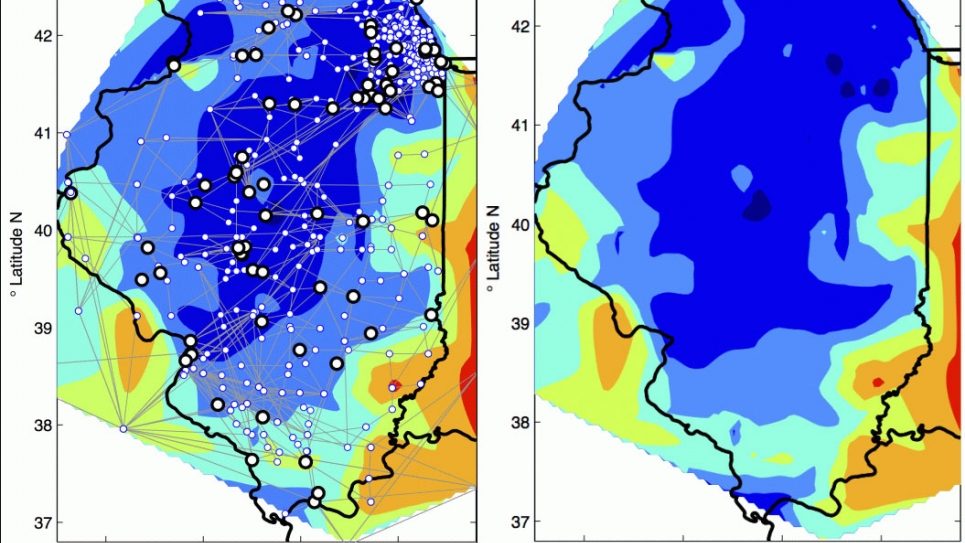
The ultimate goal of the researchers is to be able to solve power grid stochastic optimization problems in real time, and in the case of the unit commitment problems, real time means under one hour. However, the unit commitment formulations use binary (integer) variables and solving them in real time is a daunting task. The objectives and plans are to implement capabilities for solving problems involving binary (integer) decisions, and, in an effort to further improve the time to solution, to develop and implement asynchronous methods. The researchers also want to solve a full-resolution stochastic model set up for a vast geographical area (Midwest network) to assess the relationship between various facets of complex energy systems such as stochasticity, renewable energy, economic cost, and reliability.

High-performance computing will enable the researchers to incorporate larger geographical domains, longer forecast horizons, and higher temporal resolutions to maximize the power grid responsiveness. To tackle these challenges, the efforts will be focused primarily on improving time-to-solution and developing scalable capabilities for the solution of integer stochastic optimization problems. The description of this relationship will generate useful insights for policy-makers and players in the power grid and renewable energy industry.