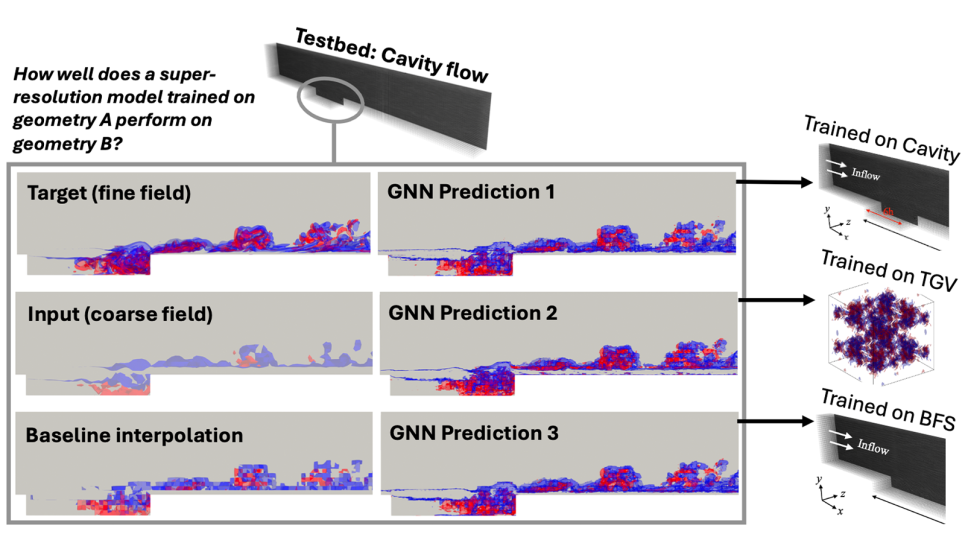
Visualizations of vorticity contours for the cavity flow at Reynolds number 1600 show examples of GNN fine-scale reconstruction and geometry extrapolation capability. (Image: Shivam Barwey, Argonne National Laboratory)
Capturing the complex behavior of turbulent flows is essential for advancing applications in energy, propulsion, power generation, and manufacturing, but simulating these flows at high resolution can be extremely costly with traditional methods. To address this challenge, researchers at Argonne National Laboratory are using ALCF computing resources to develop advanced AI models based on graph neural networks (GNN) that enhance the accuracy and efficiency of fluid flow simulations.
Turbulent flows span a wide range of spatial and temporal scales, making them challenging to simulate accurately and efficiently. High-resolution simulations that resolve this multiscale behavior require significant computing power, particularly for problems with complex geometries. Traditional coarse-grid models reduce computational cost but can miss critical flow features, while conventional super-resolution methods are incompatible with unstructured meshes in three spatial dimensions used in realistic scientific applications. Bridging this gap requires a framework that is both data-driven and mesh-aware, providing the capability to resolve localized flow structures across varied geometries.
Using the ALCF’s Polaris supercomputer, the researchers developed a multiscale GNN architecture designed to achieve super-resolution on unstructured meshes. Instead of processing entire flow fields, the model focuses on small, localized patches of simulation data, learning to reconstruct more detailed velocity fields. The network uses a combination of message-passing layers and an unpooling layer to map information between coarse and fine scales. To train and validate the model, the researchers generated high-fidelity simulation data using Argonne’s GPU-accelerated NekRS flow solver on Polaris. GNN training was distributed across multiple GPUs to efficiently process large datasets from canonical and complex flows, including Taylor–Green vortex, backward-facing step, and cavity configurations.
The team’s GNN model accurately reconstructed high-resolution flow fields from coarse inputs across all test cases, outperforming traditional interpolation methods. Key flow features and energy spectra were preserved, with model performance improving when more information from neighboring elements was included. At higher Reynolds numbers, reconstruction errors increased as expected due to greater turbulence complexity, but the model maintained consistent accuracy trends across configurations. Importantly, models trained on one geometry (e.g., backward-facing step) generalized well to others (e.g., cavity) without retraining, demonstrating strong extrapolation capabilities.
This work introduces a flexible and scalable AI-driven framework for enhancing fluid flow simulations. By capturing detailed flow behavior without the full cost of direct numerical simulation, the team’s method can accelerate modeling and design in areas such as aerospace engineering and combustion engines. The team’s research also highlights how AI and high-performance computing can be integrated to advance multiscale modeling in computational fluid dynamics.
Barwey, S., P. Pal, S. Patel, R. Balin, B. Lusch, V. Vishwanath, R. Maulik, and R. Balakrishnan. “Mesh-Based Super-Resolution of Fluid Flows with Multiscale Graph Neural Networks,” Computer Methods in Applied Mechanics and Engineering (August 2025), Elsevier.
https://doi.org/10.1016/j.cma.2025.118072